Modeling of cohesive interface: contact, interlocking, and dilatancy
Elio Sacco, University of Naples Federico II, Italy
The modeling of cohesive interfaces plays a fundamental role in mechanics, as interfaces are successfully adopted in a wide range of engineering applications at different scales (from nano- to macro-scales), including adhesive bonding, composite materials, and fracture mechanics. The literature concerning the modeling of cohesive interfaces and of their use in the different fields of the application is absolutely huge. Most of the interface models are based on the kinematics defined by the relative displacement s occurring at the two surfaces defining the interface, so that the conjugate stress quantity is the traction τ arising on these surfaces. The interface models mostly investigate the relationship between the relative displacement s and the traction τ, considering the degradation of the link between the two surfaces constituting the interface. Certainly, the interface modeling starts from the pioneering works concerning the fracture mechanics developed by Hillerborg et al. [3].
A satisfactory cohesive interface model have to account some fundamental phenomena: the effect in the degradation process of the coupling between the normal and tangential stresses, i.e. the mixity of the crack opening; the unilateral effect arising for non-monotone, e.g. cyclic, loading histories, due to the possible crack re-closure in compression; the frictional effect due to the shear sliding of the surfaces defining the crack when they are in contact (i.e. in compression); the dilatancy of the interface during the frictional sliding, which should have a limited range.
Some pioneering works [5, 8, 2, 6] accounting for some or all the above cited phenomena are reviewed and reformulated, remarking the different mechanical responses for some interesting loading history.
Then, the model proposed by Alfano and Sacco [1], coupling the damage and friction by developing a micromechanical analysis, is illustrated. The initial Alfano-Sacco interface model has been successively improved for accounting of the effects of the dilatancy and interlocking [7]. As for the original model, the mechanical response of the interface has been derived developing a micromechanical analysis in the framework of 2D and 3D rough surfaces in contact and adhesion.
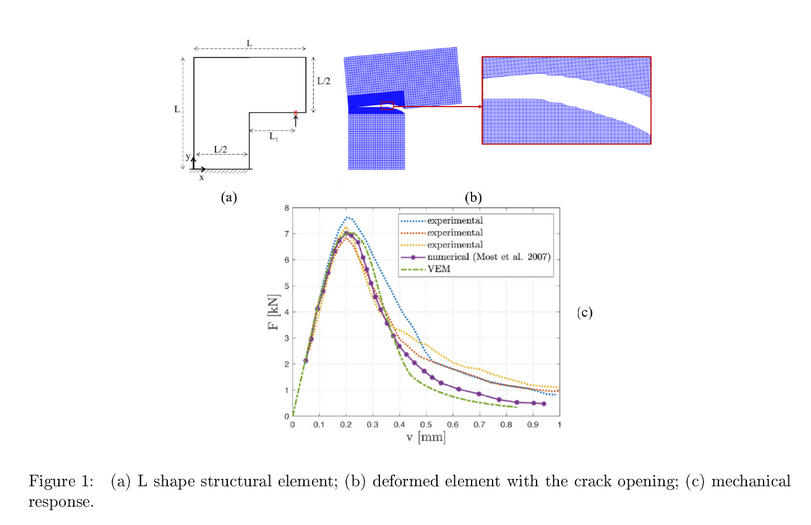
Recently, the Alfano-Sacco interface model has been implemented in a Virtual Element Method code to study the nucleation and evolution of the fracture in a cohesive solid [4]. In figure 1, a numerical result concerning a L shape structural element is schematically illustrated.
References
[1] G. Alfano and Elio Sacco. Combining interface damage and friction in a cohesive-zone model. Inter- national Journal for Numerical Methods in Engineering, 68(5):542-582, 2006.
[2] J. L. Chaboche, R. Girard, and A. Schaff. Numerical analysis of composite systems by using inter- phase/interface models. Computational Mechanics, 20(1-2):3-11, jul 1997.
[3] A. Hillerborg, M. Modéer, and P.-E. Petersson. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research, 6(6):773- 781, nov 1976.
[4] S. Marfia, E. Monaldo, and E. Sacco. Cohesive fracture evolution within virtual element method.
Engineering Fracture Mechanics, 269:108464, jun 2022.
[5] A. Needleman. A continuum model for void nucleation by inclusion debonding. Journal of Applied Mechanics, 54(3):525-531, sep 1987.
[6] M. Paggi, A. Carpinteri, and G. Zavarise. A unified interface constitutive law for the study of fracture and contact problems in heterogeneous materials. In Analysis and Simulation of Contact Problems, pages 297-304. Springer-Verlag, 2006.
[7] R. Serpieri, M. Albarella, and E. Sacco. A 3d two-scale multiplane cohesive-zone model for mixed-mode fracture with finite dilation. Computer Methods in Applied Mechanics and Engineering, 313:857-888, jan 2017.
[8] V. Tvergaard. Effect of fibre debonding in a whisker-reinforced metal. Materials Science and Engi- neering: A, 125(2):203-213, jun 1990.